A matrix is a two-dimensional data structure where numbers are arranged into rows and columns. For example,
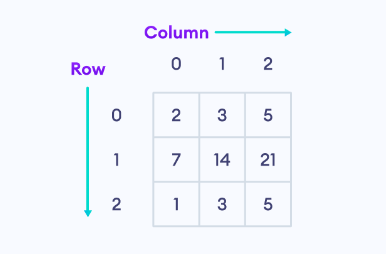
The above matrix is a 3x3 (pronounced "three by three") matrix because it has 3 rows and 3 columns.
NumPy Matrix Operations
Here are some of the basic matrix operations provided by NumPy.
| Functions | Descriptions |
|---|---|
array() |
creates a matrix |
dot() |
performs matrix multiplication |
transpose() |
transposes a matrix |
linalg.inv() |
calculates the inverse of a matrix |
linalg.det() |
calculates the determinant of a matrix |
flatten() |
transforms a matrix into 1D array |
Create Matrix in NumPy
In NumPy, we use the np.array() function to create a matrix. For example,
import numpy as np
# create a 2x2 matrix
matrix1 = np.array([[1, 3],
[5, 7]])
print("2x2 Matrix:\n",matrix1)
# create a 3x3 matrix
matrix2 = np.array([[2, 3, 5],
[7, 14, 21],
[1, 3, 5]])
print("\n3x3 Matrix:\n",matrix2)
Output
2x2 Matrix: [[1 3] [5 7]] 3x3 Matrix: [[ 2 3 5] [ 7 14 21] [ 1 3 5]]
Here, we have created two matrices: 2x2 matrix and 3x3 matrix by passing a list of lists to the np.array() function respectively.
Perform Matrix Multiplication in NumPy
We use the np.dot() function to perform multiplication between two matrices.
Let's see an example.
import numpy as np
# create two matrices
matrix1 = np.array([[1, 3],
[5, 7]])
matrix2 = np.array([[2, 6],
[4, 8]])
# calculate the dot product of the two matrices
result = np.dot(matrix1, matrix2)
print("matrix1 x matrix2: \n",result)
Output
matrix1 x matrix2: [[14 30] [38 86]]
In this example, we have used the np.dot(matrix1, matrix2) function to perform matrix multiplication between two matrices: matrix1 and matrix2.
To learn more about Matrix multiplication, please visit NumPy Matrix Multiplication.
Note: We can only take a dot product of matrices when they have a common dimension size. For example, For A = (M x N) and B = (N x K) when we take a dot product of C = A . B the resulting matrix is of size C = (M x K).
Transpose NumPy Matrix
The transpose of a matrix is a new matrix that is obtained by exchanging the rows and columns. For 2x2 matrix,
Matrix:
a11 a12
a21 a22
Transposed Matrix:
a11 a21
a12 a22
In NumPy, we can obtain the transpose of a matrix using the np.transpose() function. For example,
import numpy as np
# create a matrix
matrix1 = np.array([[1, 3],
[5, 7]])
# get transpose of matrix1
result = np.transpose(matrix1)
print(result)
Output
[[1 5] [3 7]]
Here, we have used the np.transpose(matrix1) function to obtain the transpose of matrix1.
Note: Alternatively, we can use the .T attribute to get the transpose of a matrix. For example, if we used matrix1.T in our previous example, the result would be the same.
Calculate Inverse of a Matrix in NumPy
In NumPy, we use the np.linalg.inv() function to calculate the inverse of the given matrix.
However, it is important to note that not all matrices have an inverse. Only square matrices that have a non-zero determinant have an inverse.
Now, let's use np.linalg.inv() to calculate the inverse of a square matrix.
import numpy as np
# create a 3x3 square matrix
matrix1 = np.array([[1, 3, 5],
[7, 9, 2],
[4, 6, 8]])
# find inverse of matrix1
result = np.linalg.inv(matrix1)
print(result)
Output
[[-1.11111111 -0.11111111 0.72222222] [ 0.88888889 0.22222222 -0.61111111] [-0.11111111 -0.11111111 0.22222222]]
Note: If we try to find the inverse of a non-square matrix, we will get an error message: numpy.linalg.linalgerror: Last 2 dimensions of the array must be square
Find Determinant of a Matrix in NumPy
We can find the determinant of a square matrix using the np.linalg.det() function to calculate the determinant of the given matrix.
Suppose we have a 2x2 matrix A:
a b
c d
So, the determinant of a 2x2 matrix will be:
det(A) = ad - bc
where a, b, c, and d are the elements of the matrix.
Let's see an example.
import numpy as np
# create a matrix
matrix1 = np.array([[1, 2, 3],
[4, 5, 1],
[2, 3, 4]])
# find determinant of matrix1
result = np.linalg.det(matrix1)
print(result)
Output
-5.00
Here, we have used the np.linalg.det(matrix1) function to find the determinant of the square matrix matrix1.
Flatten Matrix in NumPy
Flattening a matrix simply means converting a matrix into a 1D array.
To flatten a matrix into a 1-D array we use the array.flatten() function. Let's see an example.
import numpy as np
# create a 2x3 matrix
matrix1 = np.array([[1, 2, 3],
[4, 5, 7]])
result = matrix1.flatten()
print("Flattened 2x3 matrix:", result)
Output
Flattened 2x3 matrix: [1 2 3 4 5 7]
Here, we have used the matrix1.flatten() function to flatten matrix1 into a 1D array, without compromising any of its elements