Binary Search is a searching algorithm for finding an element's position in a sorted array.
In this approach, the element is always searched in the middle of a portion of an array.
Binary search can be implemented only on a sorted list of items. If the elements are not sorted already, we need to sort them first.
Binary Search Working
Binary Search Algorithm can be implemented in two ways which are discussed below.
- Iterative Method
- Recursive Method
The recursive method follows the divide and conquer approach.
The general steps for both methods are discussed below.
- The array in which searching is to be performed is:
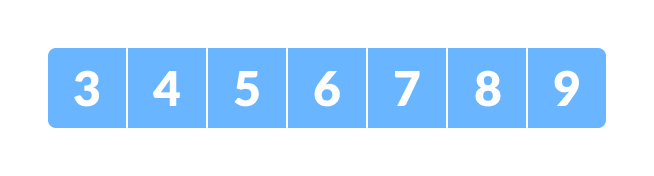
Initial array
Letx = 4be the element to be searched. - Set two pointers low and high at the lowest and the highest positions respectively.
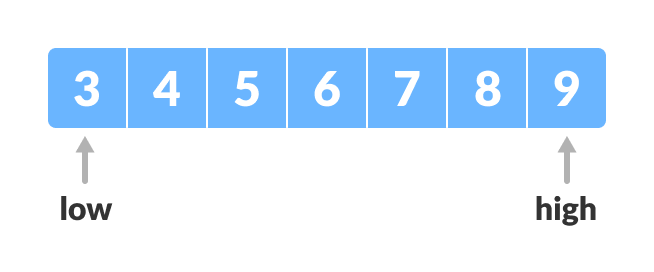
Setting pointers - Find the middle element mid of the array ie.
arr[(low + high)/2] = 6.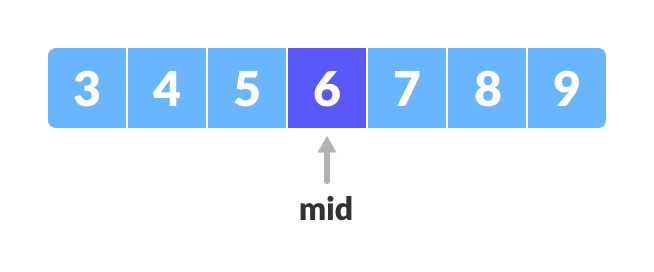
Mid element - If x == mid, then return mid.Else, compare the element to be searched with m.
- If
x > mid, compare x with the middle element of the elements on the right side of mid. This is done by setting low tolow = mid + 1. - Else, compare x with the middle element of the elements on the left side of mid. This is done by setting high to
high = mid - 1.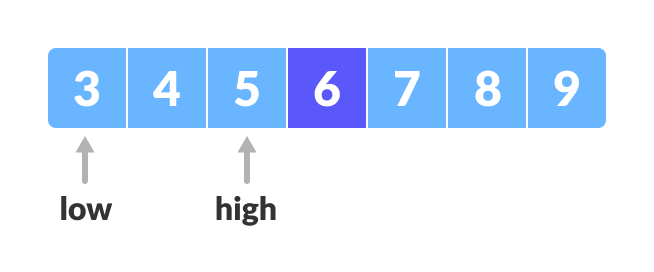
Finding mid element - Repeat steps 3 to 6 until low meets high.
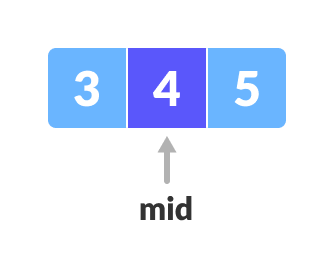
Mid element x = 4is found.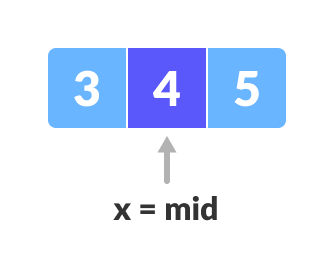
Found
Binary Search Algorithm
Iteration Method
do until the pointers low and high meet each other.
mid = (low + high)/2
if (x == arr[mid])
return mid
else if (x > arr[mid]) // x is on the right side
low = mid + 1
else // x is on the left side
high = mid - 1
Recursive Method
binarySearch(arr, x, low, high)
if low > high
return False
else
mid = (low + high) / 2
if x == arr[mid]
return mid
else if x > arr[mid] // x is on the right side
return binarySearch(arr, x, mid + 1, high)
else // x is on the left side
return binarySearch(arr, x, low, mid - 1)
Python, Java, C/C++ Examples (Iterative Method)
# Binary Search in python
def binarySearch(array, x, low, high):
# Repeat until the pointers low and high meet each other
while low <= high:
mid = low + (high - low)//2
if array[mid] == x:
return mid
elif array[mid] < x:
low = mid + 1
else:
high = mid - 1
return -1
array = [3, 4, 5, 6, 7, 8, 9]
x = 4
result = binarySearch(array, x, 0, len(array)-1)
if result != -1:
print("Element is present at index " + str(result))
else:
print("Not found")
// Binary Search in Java
class BinarySearch {
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
public static void main(String args[]) {
BinarySearch ob = new BinarySearch();
int array[] = { 3, 4, 5, 6, 7, 8, 9 };
int n = array.length;
int x = 4;
int result = ob.binarySearch(array, x, 0, n - 1);
if (result == -1)
System.out.println("Not found");
else
System.out.println("Element found at index " + result);
}
}
// Binary Search in C
#include <stdio.h>
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int n = sizeof(array) / sizeof(array[0]);
int x = 4;
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
return 0;
}
// Binary Search in C++
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}
Python, Java, C/C++ Examples (Recursive Method)
# Binary Search in python
def binarySearch(array, x, low, high):
if high >= low:
mid = low + (high - low)//2
# If found at mid, then return it
if array[mid] == x:
return mid
# Search the left half
elif array[mid] > x:
return binarySearch(array, x, low, mid-1)
# Search the right half
else:
return binarySearch(array, x, mid + 1, high)
else:
return -1
array = [3, 4, 5, 6, 7, 8, 9]
x = 4
result = binarySearch(array, x, 0, len(array)-1)
if result != -1:
print("Element is present at index " + str(result))
else:
print("Not found")
// Binary Search in Java
class BinarySearch {
int binarySearch(int array[], int x, int low, int high) {
if (high >= low) {
int mid = low + (high - low) / 2;
// If found at mid, then return it
if (array[mid] == x)
return mid;
// Search the left half
if (array[mid] > x)
return binarySearch(array, x, low, mid - 1);
// Search the right half
return binarySearch(array, x, mid + 1, high);
}
return -1;
}
public static void main(String args[]) {
BinarySearch ob = new BinarySearch();
int array[] = { 3, 4, 5, 6, 7, 8, 9 };
int n = array.length;
int x = 4;
int result = ob.binarySearch(array, x, 0, n - 1);
if (result == -1)
System.out.println("Not found");
else
System.out.println("Element found at index " + result);
}
}
// Binary Search in C
#include <stdio.h>
int binarySearch(int array[], int x, int low, int high) {
if (high >= low) {
int mid = low + (high - low) / 2;
// If found at mid, then return it
if (array[mid] == x)
return mid;
// Search the left half
if (array[mid] > x)
return binarySearch(array, x, low, mid - 1);
// Search the right half
return binarySearch(array, x, mid + 1, high);
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int n = sizeof(array) / sizeof(array[0]);
int x = 4;
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}
// Binary Search in C++
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
if (high >= low) {
int mid = low + (high - low) / 2;
// If found at mid, then return it
if (array[mid] == x)
return mid;
// Search the left half
if (array[mid] > x)
return binarySearch(array, x, low, mid - 1);
// Search the right half
return binarySearch(array, x, mid + 1, high);
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}
Binary Search Complexity
Time Complexities
- Best case complexity:
O(1) - Average case complexity:
O(log n) - Worst case complexity:
O(log n)
Space Complexity
The space complexity of the binary search is O(1).
Binary Search Applications
- In libraries of Java, .Net, C++ STL
- While debugging, the binary search is used to pinpoint the place where the error happens.